Crushing Fantasy Sports Leaderboard

by pritish jadhav - Mon, 03 Dec 2018
Tags: #python #Integer Linear Programming #Fantasy Sports #dream11 prediction #resource allocation

Crushing Fantasy Sports Leaderboard

Leverage historical data and Integer Linear Programming for selecting an optimal fantasy team.

  • Sports have played a pivotal role in our society for ages. It has been an active medium for entertainment and a means for uniting people.

  • Sports have given us legends who are followed, loved, and worshipped across the globe.

  • Over the last few years, the emergence of fantasy sports platforms has allowed fans to connect with sports on a deeper level.

  • According to a recent report published by Businesswire, North American Fantasy Sports Markets are expected to grow at a staggering CAGR of 10.7% over the next five years.

  • The story is no different in India, Asia. The fantasy sports platform, Dream11, has grown its user base by a jaw-dropping 6000% from a few lakh in 2015 users to over eight crore active users in 2020.

  • Selecting a fantasy team that is capable of earning the maximum points is not trivial. Often, emotions take over and your team ends up at the bottom of the points table in the fantasy league.

  • In this blog post, we shall explore a data-driven approach for selecting the fantasy team objectively given historical data.


Data Description -

  • For the sake of this blog, let’s focus on the game of cricket. Technically, once we have chalked out the details it is trivial to extend the logic for other sports.
  • I have managed to dump the historical fantasy points data for two of the biggest teams in the Indian Premier League (IPL), Chennai Super Kings and Mumbai Indians, in a CSV file.

The input file for auto-selecting players has the following fields -

  1. Cost - Most of the fantasy websites (including Dream11) allocate a total budget which cannot be exceeded.
  2. last_5_matches_points - This field is a list of points accrued by a player in his last 5 matches.
  3. player_category - This field highlights the category of the player. In the case of cricket, the possible categories are wicket-keeper, batsman, all-rounder, bowler. For a sport like football, the possible categories are - Goalkeeper, Defender, Midfielder, Striker. This field is important because every fantasy website restricts the number of players one can select from each of these categories.
  4. player_name - This field highlights the player name on a fantasy sports website.
  5. team_name - This column in the data frame highlights the team name of the player.

Let's get right to it by loading and inspecting the player data for an upcoming match between Chennai Superkings vs Mumbai Indians.

In [1]:
##import python libraries

from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "none"

from IPython.display import display
from IPython.display import HTML

import os
import sys
import re

import pandas as pd
import numpy as np

from ast import literal_eval
import pulp
from typing import List, Dict

from sklearn.preprocessing import LabelBinarizer
from IPython.core.display import display,HTML
display(HTML('<style>.prompt{width: 0px; min-width: 0px; visibility: collapse}</style>'))
display(HTML("<style>.container { width:100% !important; }</style>"))
In [3]:
raw_player_data = pd.read_csv('https://raw.githubusercontent.com/jadhavpritish/Dream11_Predictor/master/data/dream11_performance_data.csv', converters={"last_5_matches_points": literal_eval})
display(raw_player_data[["team_name", "player_name", "player_category", "last_5_matches_points", "cost"]].style.set_properties(**{'background-color':'#f7ebcf'}))
team_name player_name player_category last_5_matches_points cost
0 CSK M.S. dhoni wicket_keeper [25, 20, 15, 30, 18] 9
1 CSK Suresh Raina batsman [30, 10, 23, 22, 16] 10
2 MI kishan wicket_keeper [17, 13, 14, 27, 35] 8.5
3 MI rohit_sharma batsman [15, 7, 9, 40, 3] 10.5
4 MI lewis batsman [20, 18, 15, 22, 20] 9.5
5 CSK rayadu batsman [38, 40, 32, 28, 41] 9
6 MI surya batsman [30, 23, 10, 18, 25] 8.5
7 CSK watson all_rounder [35, 30, 25, 7, 18] 10.5
8 MI hardik all_rounder [25, 18, 15, 25, 30] 9
9 MI krunal all_rounder [22, 10, 5, 10, 15] 9
10 CSK bravo all_rounder [27, 20, 15, 20, 15] 9
11 MI bumrah bowler [10, 20, 25, 17, 10] 9
12 MI rahman bowler [10, 0, 0, 5, 2] 8.5
13 MI markande bowler [28, 30, 20, 30, 40] 8.5
14 CSK thakur bowler [16, 10, 7, 8, 9, 15] 8.5
15 CSK chahar bowler [24, 15, 10, 20, 23] 8

What are we trying to achieve?

  • Given the player attributes and their historical fantasy sports (at least for the last five matches), we would want to select a team of 11 players such that the probability of us winning the fantasy league is maximized.
  • Certain constraints must be satisfied while selecting the fantasy team that makes the whole process engaging and exciting.

The summary of rules for selecting a cricket team on Dream11 is as follows -

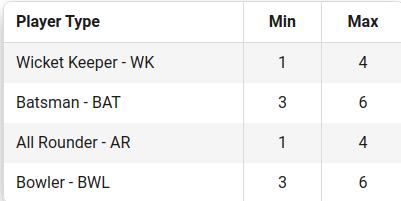
  • Every cricket team you build on Dream11 has to have an exact of 11 players. We can select a maximum of 7 players can be from the same team.

  • The captain will give you 2x points scored by them in the actual match.

  • The vice-captain will give you 1.5x points scored by them in the actual match.

Algorithm for selecting an Optimal Fantasy Team -

  • We shall frame the selection problem using Integer Linear Programming (ILP) with constraints.
  • For the sake of convenience, we shall skip the selection of caption and vice-captain in this implementation.
  • The objective function for ILP (Integer Linear Programming) will be to maximize the expected points while honoring the constraints mentioned above.
$$ \begin{equation} max \sum \limits_{i=1}^{n} [p_i \times s_i] \\ \text{S.T} \\ \text{maximum players from team 1} \implies n_{team1} \leq 7 \\ \text{maximum players from team 2} \implies n_{team2} \leq 7 \\ \text{number of wkt keepers} \implies 1 \leq n_{keepers} \leq 4 \\ \text{number of batsmen})\implies 3 \leq n_{batsmen} \leq 6 \\ \text{number of all-rounders} \implies 1 \leq n_{all-rounders} \leq 4 \\ \text{number of bowlers} \implies 3 \leq n_{bowlers} \leq 6 \\ \text{WHERE} \\ p_i \implies \text{estimated points for player i} \\ x_i \implies \text{Selection decision variable for player i [0,1]} \\ \end{equation} $$
  • Once we define the ILP problem in python, we shall use the PuLP library in python for solving the problem.

So without further adieu, let’s get down to coding.

Data Preprocessing -

1. Handling Categorical Variables

  • The team_name and player_category columns in our data are categorical features.
  • For specifying the constraints on our ILP objective function, we need to convert these features into one-hot encoded vectors. A single line of python code helps us achieve this.
In [22]:
def get_dummies(data, col_names = ["player_category", "team_name"]):
    dummies_data = pd.get_dummies(raw_player_data, columns=col_names)
    return dummies_data

processed_player_data = pd.get_dummies(raw_player_data, columns=["player_category", "team_name"])
 
display(processed_player_data.drop(['cost', 'last_5_matches_points'], axis = 1).head().style.set_properties(**{'background-color':'#f7ebcf'}))
player_name player_category_all_rounder player_category_batsman player_category_bowler player_category_wicket_keeper team_name_CSK team_name_MI
0 M.S. dhoni 0 0 0 1 1 0
1 Suresh Raina 0 1 0 0 1 0
2 kishan 0 0 0 1 0 1
3 rohit_sharma 0 1 0 0 0 1
4 lewis 0 1 0 0 0 1

2. Computing the Estimated Points per player.

  • The objective function is designed to maximize the summation of estimated points for the fantasy team.
  • We have access to every player’s historical points, but we still need to compress them into point estimates that reflect each player’s worth.
  • A simple way to achieve this would be to compute the mean fantasy points accrued by each player over the last 5 matches.

  • However, using an averaging aggregation can be misleading because we would want to capture the recent form of a player more accurately. To achieve this, we shall leverage the weighted averaging technique.

  • To demonstrate this further, let us consider an example, say, the fantasy points scored by player-1 and player-2 in the last 5 matches are as follows -


player-1 - [10, 20 , 30 , 40 , 50]
player-2 - [50, 40 , 30, 20 , 10]

  • Computing simple averages results in an aggregated score of 30 for both players.
  • However, the data suggests that player-1 is growing in confidence and has an upward trend in his performance. On the other hand, player-2 has a downward trend in his performance.
  • By taking a simple average, we are losing an important insight.
  • If we compute the averages using time decayed weights such that the most recent performance has a higher weight as compared to older performances resulting in an aggregated score of 33.93 and 26.06 for player-1 and player-2, respectively.
  • As can be seen from the above numbers that even though both the players have amassed the same number of points, the trend in performances is now being captured with player-2 getting a higher average as compared to player-1.
  • Such subtle differences will help us build a robust model.

So, let’s compute the time decayed weighted averages for the eligible players in the dataset.

In [7]:
def compute_weighted_points(points_vector, alpha = 0.20):
    
    # compute weights such that recent values are assigned a higher weight as compared to the older values. 
    weights = np.exp(list(reversed(np.array(range(1, len(points_vector)+1))*alpha * -1)))
    exponential_weighted_average = np.average(np.array(points_vector), weights = weights)
    return exponential_weighted_average

processed_player_data['weighted_player_points'] = processed_player_data['last_5_matches_points'].apply(compute_weighted_points)
processed_player_data.reset_index(inplace = True)
display(processed_player_data[['player_name', 'last_5_matches_points', 'weighted_player_points']].style.set_properties(**{'background-color':'#f7ebcf'}))
player_name last_5_matches_points weighted_player_points
0 M.S. dhoni [25, 20, 15, 30, 18] 21.4574
1 Suresh Raina [30, 10, 23, 22, 16] 19.6139
2 kishan [17, 13, 14, 27, 35] 23.3034
3 rohit_sharma [15, 7, 9, 40, 3] 15.016
4 lewis [20, 18, 15, 22, 20] 19.1937
5 rayadu [38, 40, 32, 28, 41] 35.6739
6 surya [30, 23, 10, 18, 25] 20.8027
7 watson [35, 30, 25, 7, 18] 20.842
8 hardik [25, 18, 15, 25, 30] 23.4099
9 krunal [22, 10, 5, 10, 15] 12.0189
10 bravo [27, 20, 15, 20, 15] 18.507
11 bumrah [10, 20, 25, 17, 10] 16.1006
12 rahman [10, 0, 0, 5, 2] 3.03595
13 markande [28, 30, 20, 30, 40] 30.6877
14 thakur [16, 10, 7, 8, 9, 15] 10.8823
15 chahar [24, 15, 10, 20, 23] 18.6666

Now, let's define the constraints for selecting players as defined by Dream11. These constraints are to be honored by the algorithm while trying to maximize points.

For more information, check out dream11 FAQs.

In [15]:
# Initialize the optimization Problem 
prob = pulp.LpProblem('Dreamteam', pulp.LpMaximize)

# selection decision variables can be 0 or 1. The number of `selection_decision_varibales` should be equal to 
# the number of players under consideration
selection_decision_variables = []

for row in processed_player_data.itertuples(index=True):
    variable_name = 'x_{}'.format(str(row.Index))
    variable = pulp.LpVariable(variable_name, lowBound = 0, upBound = 1, cat = 'Integer' ) 
    selection_decision_variables.append({"pulp_variable":variable, "player_name": row.player_name})
 
selection_decision_variables_df = pd.DataFrame(selection_decision_variables)

merged_processed_player_df = pd.merge(processed_player_data, selection_decision_variables_df, 
                                                   on = "player_name")
merged_processed_player_df["pulp_variable_name"] = merged_processed_player_df["pulp_variable"].apply(lambda x: x.name)
display(selection_decision_variables_df)
player_name pulp_variable
0 M.S. dhoni x_0
1 Suresh Raina x_1
2 kishan x_2
3 rohit_sharma x_3
4 lewis x_4
5 rayadu x_5
6 surya x_6
7 watson x_7
8 hardik x_8
9 krunal x_9
10 bravo x_10
11 bumrah x_11
12 rahman x_12
13 markande x_13
14 thakur x_14
15 chahar x_15
In [16]:
# Create the objective Function to be maximized

total_points = pulp.lpSum(merged_processed_player_df["weighted_player_points"] * selection_decision_variables_df["pulp_variable"])
prob += total_points

display(prob)

Dreamteam:
MAXIMIZE
21.4574342327*x_0 + 19.6138998634*x_1 + 18.507022734*x_10 + 16.1006207824*x_11 + 3.03595134142*x_12 + 30.6877000247*x_13 + 10.8823368063*x_14 + 18.6665650801*x_15 + 23.3033823875*x_2 + 15.0160173204*x_3 + 19.1936886525*x_4 + 35.6738860573*x_5 + 20.8026696164*x_6 + 20.8419816771*x_7 + 23.4099290007*x_8 + 12.0189162375*x_9 + 0.0
VARIABLES
0 <= x_0 <= 1 Integer
0 <= x_1 <= 1 Integer
0 <= x_10 <= 1 Integer
0 <= x_11 <= 1 Integer
0 <= x_12 <= 1 Integer
0 <= x_13 <= 1 Integer
0 <= x_14 <= 1 Integer
0 <= x_15 <= 1 Integer
0 <= x_2 <= 1 Integer
0 <= x_3 <= 1 Integer
0 <= x_4 <= 1 Integer
0 <= x_5 <= 1 Integer
0 <= x_6 <= 1 Integer
0 <= x_7 <= 1 Integer
0 <= x_8 <= 1 Integer
0 <= x_9 <= 1 Integer
In [17]:
# 1 <= n_keeper <= 4 
total_keepers = pulp.lpSum(merged_processed_player_df["player_category_wicket_keeper"] * selection_decision_variables_df["pulp_variable"])
prob += (total_keepers >= 1)
prob += (total_keepers <= 4)

# 3 <= n_batsmen <= 6 
total_batsmen = pulp.lpSum(merged_processed_player_df["player_category_batsman"] * selection_decision_variables_df["pulp_variable"])
prob += (total_batsmen >= 3)
prob += (total_batsmen <= 6)

# 1 <= n_allrounders <= 4
total_allrounders = pulp.lpSum(merged_processed_player_df["player_category_all_rounder"] * selection_decision_variables_df["pulp_variable"])
prob += (total_allrounders >= 1)
prob += (total_allrounders <= 4)

# 3 <= n_bowlers <= 6
total_bowlers = pulp.lpSum(merged_processed_player_df["player_category_bowler"] * selection_decision_variables_df["pulp_variable"])
prob += (total_bowlers >= 3)
prob += (total_bowlers <= 6)

# maximum of 11 players
total_players = pulp.lpSum(selection_decision_variables_df["pulp_variable"])
prob += (total_players == 11)

# maximum fantasy budget of 100
total_cost = pulp.lpSum(merged_processed_player_df["cost"] * selection_decision_variables_df["pulp_variable"])
prob += (total_cost <= 100)

# we cannot pick more than 7 players from the same team
total_team1 = pulp.lpSum(merged_processed_player_df["team_name_CSK"] * selection_decision_variables_df["pulp_variable"])
prob += (total_team1 <= 7)

total_team2 = pulp.lpSum(merged_processed_player_df["team_name_MI"] * selection_decision_variables_df["pulp_variable"])
prob += (total_team2 <= 7)



display(prob)
prob.writeLP('Dreamteam.lp')

assert len(pulp.listSolvers(onlyAvailable=True)) > 0, "solvers not installed correctly - check - https://www.coin-or.org/PuLP/main/installing_pulp_at_home.html"
prob.solve()

Dreamteam:
MAXIMIZE
21.4574342327*x_0 + 19.6138998634*x_1 + 18.507022734*x_10 + 16.1006207824*x_11 + 3.03595134142*x_12 + 30.6877000247*x_13 + 10.8823368063*x_14 + 18.6665650801*x_15 + 23.3033823875*x_2 + 15.0160173204*x_3 + 19.1936886525*x_4 + 35.6738860573*x_5 + 20.8026696164*x_6 + 20.8419816771*x_7 + 23.4099290007*x_8 + 12.0189162375*x_9 + 0.0
SUBJECT TO
_C1: x_0 + x_2 >= 1

_C2: x_0 + x_2 <= 4

_C3: x_1 + x_3 + x_4 + x_5 + x_6 >= 3

_C4: x_1 + x_3 + x_4 + x_5 + x_6 <= 6

_C5: x_10 + x_7 + x_8 + x_9 >= 1

_C6: x_10 + x_7 + x_8 + x_9 <= 4

_C7: x_11 + x_12 + x_13 + x_14 + x_15 >= 3

_C8: x_11 + x_12 + x_13 + x_14 + x_15 <= 6

_C9: x_0 + x_1 + x_10 + x_11 + x_12 + x_13 + x_14 + x_15 + x_2 + x_3 + x_4
 + x_5 + x_6 + x_7 + x_8 + x_9 = 11

_C10: 9 x_0 + 10 x_1 + 9 x_10 + 9 x_11 + 8.5 x_12 + 8.5 x_13 + 8.5 x_14
 + 8 x_15 + 8.5 x_2 + 10.5 x_3 + 9.5 x_4 + 9 x_5 + 8.5 x_6 + 10.5 x_7 + 9 x_8
 + 9 x_9 <= 100

_C11: x_0 + x_1 + x_10 + x_14 + x_15 + x_5 + x_7 <= 7

_C12: x_11 + x_12 + x_13 + x_2 + x_3 + x_4 + x_6 + x_8 + x_9 <= 7

VARIABLES
0 <= x_0 <= 1 Integer
0 <= x_1 <= 1 Integer
0 <= x_10 <= 1 Integer
0 <= x_11 <= 1 Integer
0 <= x_12 <= 1 Integer
0 <= x_13 <= 1 Integer
0 <= x_14 <= 1 Integer
0 <= x_15 <= 1 Integer
0 <= x_2 <= 1 Integer
0 <= x_3 <= 1 Integer
0 <= x_4 <= 1 Integer
0 <= x_5 <= 1 Integer
0 <= x_6 <= 1 Integer
0 <= x_7 <= 1 Integer
0 <= x_8 <= 1 Integer
0 <= x_9 <= 1 Integer
In [20]:
# prep solution

solutions_df = pd.DataFrame(
    [
        {
            'pulp_variable_name': v.name, 
            'value': v.varValue
        }
        for v in prob.variables()
    ]
)


result = pd.merge(merged_processed_player_df, solutions_df, on = 'pulp_variable_name')
result = result[result['value'] == 1].sort_values(by = 'weighted_player_points', ascending = False)
selected_cols_final = ['player_name', 'team_name_CSK', 'team_name_MI', 'weighted_player_points']
final_set_of_players_to_be_selected = result[selected_cols_final]

display(final_set_of_players_to_be_selected.style.set_properties(**{'background-color':'#f7ebcf'}))

print("We can accrue an estimated points of %f"%(final_set_of_players_to_be_selected['weighted_player_points'].sum()))
player_name team_name_CSK team_name_MI weighted_player_points
5 rayadu 1 0 35.6739
13 markande 0 1 30.6877
8 hardik 0 1 23.4099
2 kishan 0 1 23.3034
0 M.S. dhoni 1 0 21.4574
7 watson 1 0 20.842
6 surya 0 1 20.8027
1 Suresh Raina 1 0 19.6139
4 lewis 0 1 19.1937
15 chahar 1 0 18.6666
11 bumrah 0 1 16.1006 
We can accrue an estimated points of 249.751757

There you GO !! We have our Dream Team !!

All that needs to be done is to select the team in the app and start earning money !!

Before we wrap up this tutorial, I would like to highlight the features as well as the enhancement opportunities for the existing algorithm -

a. The existing algorithm is completely automated and spits out the Dream team that maximizes the probability of scoring the highest points.
b. In addition to that, it also conveys the estimated points that can be accrued through the selected team. The value would help us check the accuracy of the system.
c. The algorithm is sensitive to player performance trends and it adjusts accordingly.

Enhancements -
a. The input data needs to be stored in a database. Currently, I am relying on manual efforts to fetch the required data.
b. The algorithm is not sensitive to injury news and other team updates. This is a significant miss and we will have to rely on scrapping and detecting such information through NLP on sports websites. It is an open-ended question.

Comments

© 2016 Blend Free HTML5. All Rights Reserved. Designed by FreeHTML5.co
Pelican Theme by: Claudio Walser